skshape.geometry package

Submodules

skshape.geometry.curve module

Curves, curve families, and relevant geometric functionality.

This module contains the Curve and CurveHierarchy classes, and the geometric functionality, such as curvature, normal computations, etc.

class skshape.geometry.curve.Curve(coords, adaptivity_parameters={})

Bases: skshape.geometry._mesh.Mesh

Lagrangian curve discretized as a list of nodes, and geometric functions.

Curve class encapsulating the data and functionality for a Lagrangian curve discretized as a list of nodes on the (x,y) plane. The geometric functions include normal, curvature computation, interior area and other functions.

adapt(parameters=None)

area()

bounding_box()

contains(obj)

coords()

copy(copy_cache_data=False)

curvature(s=None, mask=None, coarsened=False)

Computes the curvature of the curve.

Computes the curvature at the node i by fitting a circle to nodes i-1, i, i+1 and computing its radius r. Then the curvature is given by 1/r. The curvature values between the nodes are given by linear interpolation.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the curvature is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the curvature values are sought.

• coarsened (bool, optional) – True if the curvature values are sought for coarsened elements, otherwise False.

Returns

curvature – A NumPy array storing the computed curvature values.

Return type

NumPy array

dim()

dim_of_world()

edges()

element_sizes(mask=None, coarsened=False, squared=False)

exterior_area(world_boundary=None)

exterior_volume(world_boundary=None)

interior_area(world_boundary=None)

interior_volume(world_boundary=None)

length()

move(update, adaptivity=None, world_boundary=None)

move_back()

normals(s=None, mask=None, coarsened=False, smoothness='pwconst')

Computes the unit normals of the curve.

Returns the normal vectors for the elements of a curve (the pwconst case) or for the nodes of the curve (the pwlinear case). In the piecewise constant case, the normals are given by the difference of the first and second nodes of the element, i.e.

In the piecewise linear case, the normals are computed as weighted averages of the element normals. The normal vectors are normalized to have unit length.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the normal is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the normals are sought.

• coarsened (bool, optional) – True if the normals are sought for coarsened elements, otherwise False.

• smoothness (str, optional) – An optional flag denoting the smoothness of the computed normals. Its value can be ‘pwconst’, corresponding to piecewise constant normals defined on the elements, (but not on the nodes) or its value can be ‘pwlinear’, corresponding to piecewise linear normals, defined by coefficients on the nodes and by interpolation of the coefficients on the edges.

Returns

normals – A NumPy array of size 2xN storing the x and y components of the normals.

Return type

NumPy array

orientation()

Returns the orientation of the curve.

Computes the signed area of the curve, and returns the orientation of the curve based on the area. If area > 0, then orientation is 1. If area < 0, then orientation is -1. If area = 0, then orientation is 0.

Returns

orientation_value

Return type

int, one of -1,0,1

refine_coarsen(mask, data_vecs, refinement_method='curved')

reset_data()

reverse_orientation()

safe_step_size(V, tol=0.3)

The maximum safe step size to avoid local geometric distortions.

If the spacing between the two nodes of an element changes too rapidly, this might create distortions in the geometric representation. This function computes the maximum safest step size to move the curve with the given velocity. The computation is based on the following inequality to be enforced

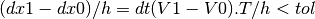
where dx1, dx0 denote the changes in the node locations, V1, V0 are their velocity, h is the size, T is the tangent vector of the element.

Parameters

• V (NumPy array) – The velocity vector, a NumPy array of size (2,n), where n is the number of nodes of the curve.

• tol (float) – Allowed ratio of relative tangential displacement with respect to the element size. The default value is 0.3.

Returns

dt – The maximum safe step size allowed within the specified tolerance.

Return type

float

second_fund_form(s=None, mask=None, coarsened=False)

Estimates the second fundamental form on nodes of the curve.

Estimates the second fundamental form on each element using the following formula:

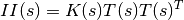
where K(s) is the scalar curvature, interpolated linearly from nodal curvature values, T(s) is piecewise linear reconstruction of the unit tangent vector, T(s)^T is its transpose. The second fundamental curve can be computed for nodes of the curve or interior points of the elements denoted by s, on all elements or selected elements specified by mask. They can be computed for coarsened elements too.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the second fundamental form is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the values of the second fundamental form are sought.

• coarsened (bool, optional) – True if the values of the second fundamental form are sought for coarsened elements, otherwise False.

Returns

II – An array of size 2x2xN storing the components of the second fundamental form.

Return type

NumPy array

set_adaptivity(adaptivity=True)

Turns on/off mesh adaptivity.

This function is used to switch mesh adaptivity on or off.

Parameters

adaptivity (bool) – A boolean argument to set mesh adaptivity to True or False.

set_data_adaptivity_criteria(refinement_functions=None, coarsening_functions=None, append=False)

Sets data adaptivity criteria given for refinement and coarsening.

Curves can be adapted spatially (refined or coarsened) with respect to given criteria. This function is used to set or add a refinement or coarsening pair (of error and marking functions) to the criteria list. The curve’s criteria list includes the geometric criterion by default (if created with default arguments).

The geometric criterion estimates the geometric error by examining the curvatures and element sizes of the curves. Then the marking function marks the elements with errors above a certain threshold for refinement. See the following function for more information:

geometry.curve_adaptivity.compute_geometric_error(...)

If new refinement or coarsening error functions are added or appended, then mesh_adaptivity is turned on. To turn it off, you need to call the function: set_adaptivity(False).

Parameters

• refinement_functions –

  A pair of pairs storing the error estimation function and the corresponding marking function to drive refinement of elements. It has the following format:

  ( error_estimation_pair, marking_pair )

  where

  error_estimation_pair = (error_func, error_params)

  and

  marking_pair = (marking_func, marking_params).

  The error estimation function should have the curve as an argument and three other optional arguments: mask, a boolean NumPy array or an integer NumPy array of element indices, vec, a float NumPy array to store the error values, parameters, a dictionary of parameters needed for error estimation. The default for these three arguments can be None. An example is

  compute_geometric_error(curve, mask=None, vec=None,

  parameters=None)

  Marking functions are defined in the module geometry.marking.

• coarsening_functions – A pair of pairs storing the error estimation function and the corresponding marking function to drive coarsening of elements. Its format is the same as that of refinement functions.

• append (bool, optiomal) – A boolean optional flag with default value equal to False. If it is True, the given criteria are appended to the existing list and all the criteria in the list are used together. If it is False, only the first geometric criteria (if they are available) are kept in the refinement and coarsening criteria list, the others in the lists are removed and the new ones are inserted.

set_geometry(coords, element_sizes=None, normals=None, curvature=None)

set_orientation(new_orientation)

show(format='b', factor=1.0)

size()

surface_area()

tangents(s=None, mask=None, coarsened=False, smoothness='pwconst')

Computes the unit tangents of the curve.

Returns the tangent vectors for the elements of a curve (the pwconst case) or for the nodes of the curve (the pwlinear case). In the piecewise constant case, the tangents are given by the difference of the first and second nodes of the element, i.e.

In the piecewise linear case, the tangents are computed as weighted averages of the element tangents. The tangent vectors are normalized to have unit length.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the tangent is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the tangents are sought.

• coarsened (bool, optional) – True if the tangents are sought for coarsened elements, otherwise False.

• smoothness (str, optional) – An optional flag denoting the smoothness of the computed tangents. Its value can be ‘pwconst’, corresponding to piecewise constant tangents defined on the elements, (but not on the nodes) or its value can be ‘pwlinear’, corresponding to piecewise linear tangents, defined by coefficients on the nodes and by interpolation of the coefficients on the edges.

Returns

tangents – A NumPy array of size 2xN storing the x and y components of the tangents.

Return type

NumPy array

volume()

class skshape.geometry.curve.CurveHierarchy(curve_list, world_boundary=None, curve_hierarchy=None, adaptivity_parameters={})

Bases: skshape.geometry._mesh.Mesh

Hierarchy of nonintersecting simple curves on the (x,y) plane.

This class stores the hierarchy and spatial positioning of a set of nonintersecting simple curves on (x,y) planes. It stores the list of the Curve objects as well. In this way, it can perform the geometric computations, e.g. curvature, normals for all the curves.

adapt(parameters=None)

add_remove_curves(remove_curve_ids, new_curve_list, recompute_parent_list=[], enforce_consistency=True)

area()

coords()

copy(copy_cache_data=False)

curvature(s=None, mask=None, coarsened=False)

Computes the curvature of the curves in the CurveHierarchy.

Computes the curvature at the node i by fitting a circle to nodes i-1, i, i+1 and computing its radius r. Then the curvature is given by 1/r. The curvature values between the nodes are given by linear interpolation.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the curvature is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the curvature values are sought.

• coarsened (bool, optional) – True if the curvature values are sought for coarsened elements, otherwise False.

Returns

curvature – A NumPy array storing the computed curvature values.

Return type

NumPy array

curve_hierarchy()

curve_list()

dim()

dim_of_world()

edges()

element_sizes(mask=None, coarsened=False, squared=False)

exterior_area(world_boundary=None)

exterior_domain(world_boundary=None)

exterior_volume(world_boundary=None)

get_curve_object(curve_id)

has_submeshes()

hole_points()

interior_area(world_boundary=None)

interior_domain(world_boundary=None)

interior_volume(world_boundary=None)

length()

local_to_global(s, mask=None, coarsened=False)

move(update, adaptivity=None, world_boundary=None)

move_back()

normals(s=None, mask=None, coarsened=False, smoothness='pwconst')

Computes the unit normals of the curve family.

Returns the normal vectors for the elements of the curves (the pwconst case) or for the nodes of the curves (the pwlinear case). In the piecewise constant case, the normals are given by the difference of the first and second nodes of the element, i.e.

In the piecewise linear case, the normals are computed as weighted averages of the element normals. The normal vectors are normalized to have unit length.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the normal is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the normals are sought.

• coarsened (bool, optional) – True if the normals are sought for coarsened elements, otherwise False.

• smoothness (str, optional) – An optional flag denoting the smoothness of the computed normals. Its value can be ‘pwconst’, corresponding to piecewise constant normals defined on the elements, (but not on the nodes) or its value can be ‘pwlinear’, corresponding to piecewise linear normals, defined by coefficients on the nodes and by interpolation of the coefficients on the edges.

Returns

normals – A NumPy array of size 2xN storing the x and y components of the normals.

Return type

NumPy array

orientation()

refine_coarsen(mask, data_vecs, refinement_method='curved')

region_areas(world_boundary=None)

region_volumes(world_boundary=None)

regions()

reset_data()

reverse_orientation()

safe_step_size(V, tol=0.3)

The maximum safe step size to avoid local geometric distortions.

If the spacing between the two nodes of an element changes too rapidly, this might create distortions in the geometric representation. This function computes the maximum safest step size to move the curve with the given velocity. The computation is based on the following inequality to be enforced

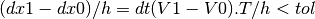
where dx1, dx0 denote the changes in the node locations, V1, V0 are their velocity, h is the size, T is the tangent vector of the element.

Parameters

• V (NumPy array) – The velocity vector, a NumPy array of size (2,n), where n is the number of nodes of the curve.

• tol (float) – Allowed ratio of relative tangential displacement with respect to the element size. The default value is 0.3.

Returns

dt – The maximum safe step size allowed within the specified tolerance.

Return type

float

second_fund_form(s=None, mask=None, coarsened=False)

Estimates the second fundamental form on nodes of the curves.

Estimates the second fundamental form on each element using the following formula:

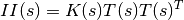
where is the scalar curvature, interpolated linearly from nodal curvature values, 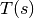is piecewise linear reconstruction of the unit tangent vector, 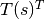is its transpose. The second fundamental curve can be computed for nodes of the curve or interior points of the elements denoted by s, on all elements or selected elements specified by mask. They can be computed for coarsened elements too.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the second fundamental form is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the values of the second fundamental form are sought.

• coarsened (bool, optional) – True if the values of the second fundamental form are sought for coarsened elements, otherwise False.

Returns

II – An array of size 2x2xN storing the components of the second fundamental form.

Return type

NumPy array

set_adaptivity(adaptivity=True)

Turns on/off mesh adaptivity.

This function is used to switch mesh adaptivity on or off.

Parameters

adaptivity (bool) – A boolean arguments to set mesh adaptivity to True or False.

set_boundary(world_boundary)

set_data_adaptivity_criteria(refinement_functions=None, coarsening_functions=None, append=False)

Sets data adaptivity criteria given for refinement and coarsening.

Curves can be adapted spatially (refined or coarsened) with respect to given criteria. This function is used to set or add a refinement or coarsening pair (of error and marking functions) to the criteria list. The curve’s criteria list includes the geometric criterion by default (if created with default arguments).

The geometric criterion estimates the geometric error by examining the curvatures and element sizes of the curves. Then the marking function marks the elements with errors above a certain threshold for refinement. See the following function for more information:

geometry.curve_adaptivity.compute_geometric_error(...)

If new refinement or coarsening error functions are added or appended, then mesh_adaptivity is turned on. To turn it off, you need to call the function: set_adaptivity(False).

Parameters

• refinement_functions –

  A pair of pairs storing the error estimation function and the corresponding marking function to drive refinement of elements. It has the following format:

  ( error_estimation_pair, marking_pair )

  where

  error_estimation_pair = (error_func, error_params)

  and

  marking_pair = (marking_func, marking_params).

  The error estimation function should have the curve as an argument and three other optional arguments: mask, a boolean NumPy array or an integer NumPy array of element indices, vec, a float NumPy array to store the error values, parameters, a dictionary of parameters needed for error estimation. The default for these three arguments can be None. An example is

  compute_geometric_error(curve, mask=None, vec=None,

  parameters=None)

  Marking functions are defined in the module geometry.marking.

• coarsening_functions – A pair of pairs storing the error estimation function and the corresponding marking function to drive coarsening of elements. Its format is the same as that of refinement functions.

• append (bool, optional) – A boolean optional flag with default value False. If it is True, the given criteria are appended to the existing list and all the criteria in the list are used together. If it is False, only the first geometric criteria (if they are available) are kept in the refinement and coarsening criteria list, the others in the lists are removed and the new ones are inserted.

set_orientation(new_orientation)

set_topology_changes(value=True)

show(format='b', factor=1.0)

size()

submeshes()

surface_area()

tangents(s=None, mask=None, coarsened=False, smoothness='pwconst')

Computes the unit tangents of the curve family.

Returns the tangent vectors for the elements of the curves (the pwconst case) or for the nodes of the curves (the pwlinear case). In the piecewise constant case, the tangents are given by the difference of the first and second nodes of the element, i.e.

In the piecewise linear case, the tangents are computed as weighted averages of the element tangents. The tangent vectors are normalized to have unit length.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the tangent is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the tangents are sought.

• coarsened (bool, optional) – True if the tangents are sought for coarsened elements, otherwise False.

• smoothness (str, optional) – An optional flag denoting the smoothness of the computed tangents. Its value can be ‘pwconst’, corresponding to piecewise constant tangents defined on the elements, (but not on the nodes) or its value can be ‘pwlinear’, corresponding to piecewise linear tangents, defined by coefficients on the nodes and by interpolation of the coefficients on the edges.

Returns

tangents – A NumPy array of size 2xN storing the x and y components of the tangents.

Return type

NumPy array

topmost_curve_ids()

volume()

skshape.geometry.curve_adaptivity module

Functions to estimate errors and adjust curve node sampling.

This module contains functions for curve adaptivity, based on geometric and data-based error estimation, implemented via curve element/edge refinement or coarsening.

skshape.geometry.curve_adaptivity.adapt(curve, parameters={'coarsening errors and marking': [], 'errors and marking': [((<function compute_geometric_error>, None), (<function fixed_el_tol_marking>, {'tolerance': 0.01, 'gamma_coarsen': 0.2}))], 'maximum element size': 1000.0, 'maximum iterations': 5, 'minimum element size': 1e-08, 'refinement method': 'curved'})

Adapts a given curve by refinement and coarsening of the curve elements.

Given a list of error estimator and marking function pairs (and their parameters) defined in the parameters argument, this function adapts the given curve, namely it refines and coarsens elements of the curve by adding or removing nodes. The adaptation is performed iteratively (up to a maximum number of iterations), by estimating element errors and marking the elements for refinement or coarsening according to the error and marking criteria. Minimum and maximum element sizes are also specified in the parameters so that the elements are not refined beyond the minimum element size or coarsened beyond the maximum element size.

Parameters

• curve (:obj:'Curve) –

• parameters –

  A dictionary of the parameters for adaptivity. It includes

  • a list of the error estimation and marking functions pairs and their parameters,

  • a list of the coarsening error estimation and marking function pairs and their parameters,

  • the maximum number of adaptation iterations,

  • the minimum element size,

  • the maximum element size,

  • the type of the refinement method (‘curved’ or ‘linear’)

  Its default value is geometric_adaptivity_parameters defined in this file. An example set of parameters is as follows:

  pair1 = ( (compute_geometric_error, None),
          (fixed_el_tol_marking, {'tolerance': 0.01,
                                  'gamma_coarsen': 0.2} ) )
  pair2 = ( (compute_data_error, {'data function':f}),
          (equidistribution_marking, {'tolerance':    0.0001,
                                      'gamma_refine': 0.7,
                                      'gamma_coarsen':0.05} ) )
  pair3 = ( (compute_data_coarsening_error,{'data function':f}),
          (equidistribution_marking, {'tolerance':    0.0001,
                                      'gamma_refine': 0.7,
                                      'gamma_coarsen':0.05} ) )
  params = { 'errors and marking': [ pair1, pair2 ],
           'coarsening errors and marking': [ pair3 ],
           'maximum iterations': 5,
           'minimum element size': 0.0001,
           'maximum element size': 1.0,
           'refinement method':'curved' }
  

  Each pair defined above includes two pairings. One is the error estimation function and its parameters, the other is the marking function id and its parameters. The error estimation functions should have the curve as an argument and three other optional arguments: mask, a boolean NumPy array or an integer NumPy array of element indices, vec, a float NumPy array to store the error values, parameters, a dictionary of parameters needed for error estimation. The default for these three arguments can be None. An example is

Returns

adapted – A boolean value that is True if the curve has been adapted (refined or coarsened), False if the curve has not been adapted.

Return type

bool

skshape.geometry.curve_adaptivity.compute_data_coarsening_error(curve, mask=None, vec=None, parameters=None)

Estimates the integration error on each element in the case of coarsening.

This function computes an approximation to the integration error on each element for a given mesh function f after coarsening the curve. For example, if the current element is given by (X[i],X[i+1]) and its next element is (X[i+1],X[i+2]) (X being the coordinates of the nodes), then the coarsened element would be (X[i],X[i+2]), and these are element coordinates used for computation. The integration error is estimated by performing quadratures of order 0 and 1 on each coarsened element, scaling the quadrature sums by element sizes and taking the difference of the results for 0 and 1.

If the mask vector is given, then error is computed for only the elements specified by mask.

If vec is provided the user, the computed values are stored in vec and vec is returned as the error vector.

The parameters for this function have to be specified and should include the data function f that is being integrated.

Parameters

• curve (:obj:'Curve) –

• mask (boolean or integer NumPy array, optional) – An optional argument to be provided if the error is computed for some of the elements only. It can be a boolean NumPy array of the same size as the curve or it can be an integer NumPy array of element indices.

• vec (NumPy array, optional) – An optional output vector. If it is provided, then the computed error values are written to vec, and vec is returned is the error vector.

• parameters (dict) – An parameter dictionary that has to be provided. Its format is: {‘data function’:f}, where f is an instance of a MeshFunction; f should be able to take the arguments in the form f(curve,s,mask,coarsened), where s is the local parametric coordinate on the element in the interval [0,1].

Returns

error – The computed error values for all elements. It is the same size as the curve.

Return type

NumPy array

skshape.geometry.curve_adaptivity.compute_data_error(curve, mask=None, coarsened=False, vec=None, parameters=None)

Computes the integration error for given f on each element.

This function computes an approximation to the integration error on each element for a given mesh function f. The integration error is estimated by performing high and low order quadratures on each element, multiplying the quadrature sums by element sizes and taking the difference of the results for the high and low orders (default values 2 and 3 respectively). The error estimates are normalized by dividinng by curve length.

If the mask vector is given, then error is computed for only the elements specified by mask.

If vec is provided the user, the computed values are stored in vec and vec is returned as the error vector. Otherwise a new Numpy array is allocated as the error vector.

The parameters for this function have to be specified and should include the data function f that is being integrated. The function f can be a MeshFunction defined on the curve.

If coarsen is set to be True, then the error values are not computed for the existing elements of the curve. They are computed for the elements that would result from the coarsening of the current elements. For example, if the current element is given by (X[i],X[i+1]) and its next element is (X[i+1],X[i+2]) (X being the coordinates of the nodes), then the coarsened element would be (X[i],X[i+2]), and these are element coordinates used for computation when coarsened=True.

Parameters

• curve (:obj:'Curve') –

• mask (boolean or integer NumPy array, optional) – An optional argument to be provided if the error is computed for some of the elements only. It can be a boolean NumPy array of the same size as the curve or it can be an integer NumPy array of element indices.

• coarsened (bool, optional) – An optional boolean value that indicates whether the errors are being computed for the current elements (coarsened=False), or for those obtained by coarsening the current elements (coarsened=True).

• vec (NumPy array, optional) – An optional output vector. If it is provided, then the computed error values are written to vec, and vec is returned is the error vector.

• parameters (dict) – An parameter dictionary that has to be provided. Its format is: {‘data function’:f,’low quadrature’:order0,’high quadrature’:order1}, where f is an instance of a MeshFunction; f should be able to take the arguments in the form f(curve,s,mask,coarsened), where s is the local parametric coordinate on the element in the interval [0,1]. The quadrature orders, order0 and order1, are optional integer values.

Returns

error – The computed error values for all elements. It is the same size as the curve.

Return type

NumPy array

skshape.geometry.curve_adaptivity.compute_geometric_error(curve, mask=None, coarsened=False, vec=None, parameters=None)

Computes the discretization error for a given Curve object.

This function takes a Curve object as input and returns an estimate of the maximum pointwise error per element, incurred by the geometric discretization represented by the Curve object. To be specific, the output is the error vector defined as follows

error[i] = max|X(s) - x(s)| for all s on element[i],

where X(s) is the true curve coordinate and x(s) is the coordinate given by the discretized curve representation. The actual error is computed by the following estimate

error[i] = max{K1,K2} h^2,

where K1,K2 are the curvature values at the 1st and 2nd nodes of the element[i] respectively, and h is the size of the element.

If a mask vector is given, the error is computed only for the elements specified by mask.

If the argument vec is given, the error is returned in vec. Otherwise a new Numpy array is allocated as the error vector.

If coarsen is set to be True, then the error values are not computed for the existing elements of the curve. They are computed for the elements that would result from the coarsening of the current elements. For example, if the current element is given by (X[i],X[i+1]) and its next element is (X[i+1],X[i+2]) (X being the coordinates of the nodes), then the coarsened element would be (X[i],X[i+2]), and these are element coordinates used for computation when coarsened=True.

Parameters

• curve (:obj:'Curve') – A instance of a Curve class, storing the curve geometry.

• mask (NumPy array, optional) – An optional argument to be provided if the error is computed for some of the elements only. It can be a boolean NumPy array of the same size as the curve or it can be an integer NumPy array of element indices.

• coarsened (bool, optional) – True if the errors are being computed for coarsened elements, otherwise False.

• vec (NumPy array, optional) – An optional output vector. If it is provided, then the computed error values are written to vec, and vec is returned is the error vector.

• parameters (dict, optional) – An optional and unused argument, included in the function definition for compatibility.

Returns

error – A NumPy array of real numbers, storing the computed error values for all elements. It is the same size as the curve.

Return type

NumPy array

skshape.geometry.curve_adaptivity.copy_adaptivity_parameters(params=None, new_curves=None)

skshape.geometry.curve_adaptivity.estimates_and_markers(curve, current_info, parameters)

Estimates the errors of elements and marks them for refinement/coarsening.

This function executes a set of error estimator functions specified in the parameters and computes the error values for each element. Once each error estimator is executed, the corresponding marking function is also executed. The elements with high errors are marked as 1 for refinement and those with too low error are marked as -1 for coarsening (the remaining elements are marked as 0).

A set of functions for coarsening error (and their corresponding marking functions) can also be provided in parameters. These function are executed only on the elements marked for coarsening. If the coarsening error is too high, these elements are unmarked, i.e. the corresponding locations in the markers array are set to 0.

Parameters

• curve (:obj:'Curve') –

• current_info (tuple of list of NumPy arrays) – A pair of a list of error vectors and a NumPy array of integer indices indicating which elements have been updated. If this information is not available, its value is None. The error vectors should be as many as the error functions specified in parameters. Each error vector is a NumPy array of real values with a length equal to the size of the curve. The error vectors can contain previously computed error values or ‘nan’ values indicating invalid or uncomputed values.

• parameters (dict) –

  A dictionary of parameters that should contain the error functions and the corresponding marking functions (from geometry.marking), paired with their parameters. Optionally it also contains the coarsening error function. The following is an example dictionary of parameters:

  pair1 = ( (compute_geometric_error, None),
          (fixed_el_tol_marking, {'tolerance': 0.01,
                                  'gamma_coarsen': 0.2} ) )
  pair2 = ( (compute_data_error, {'data function':f}),
          (equidistribution_marking, {'tolerance':    0.0001,
                                      'gamma_refine': 0.7,
                                      'gamma_coarsen':0.05} ) )
  pair3 = ( (compute_coarsen_error,{'data function':f}),
          (equidistribution_marking, {'tolerance':    0.0001,
                                      'gamma_refine': 0.7,
                                      'gamma_coarsen':0.05} ) )
  params = { 'errors and marking': [ pair1, pair2 ],
           'coarsening errors and marking': [ pair3 ] }
  

Returns

markers – Array of integer markers with length equal to curve size. If element[i] is to be refined, then markers[i] = 1. If element[i] is to be coarsened, then markers[i] = -1. Otherwise markers[i] = 0.

Return type

NumPy array

skshape.geometry.curve_adaptivity.geometric_adaptivity_parameters()

Returns a new copy of the geometric adaptivity parameters for curves.

Returns a new copy of the geometric adaptivity parameters for curves. This is a dictionary with the following content.

Returns

parameters – A copy of the following dictionary of parameters.

{ 'maximum iterations': 5,
  'minimum element size': 1e-8,
  'maximum element size': 1000.0,
  'refinement method':'curved'
  'errors and marking': [
      ( (compute_geometric_error, None),
        (fixed el tol_marking,
         marking_default_parameters['fixed element tol']) ) ],
  'coarsening errors and marking': []  }

Return type

dict

skshape.geometry.curve_adaptivity.refine_coarsen(curve, markers, data_vectors, refinement_method='curved')

Refines/coarsens elements of a curve following a given markers array.

Given a curve object and an array of markers, this function refines (adds nodes) and coarsens (removes nodes) the elements of the curve. Adding and removing nodes changes the ordering of the coordinates of the curve’s nodes. For example, if the old node indices are 0,1,2,3,4 and the elements are (0,1),(1,2),(2,3),(3,4),(4,0), then with a markers array of [1,-1,0,1,0], the changes in the elements is:

(0,1) refine => (0,1.5),(1.5,1) remapped to (0,1),(1,2)

(1,2),(2,3) coarsen => (1,3) remapped to (2,3)

(3,4) refine => (3,3.5),(3.5,4) remapped to (3,4),(4,5)

(4,0) no change => (4,0) remapped to (5,0)

The nodes of the new curve are 0,1,2,3,4,5 and the elements are (0,1),(1,2),(2,3),(3,4),(4,5),(5,0).

If some data is associated with the old elements (specified in the list of arrays, data_vectors), it can be reassigned to the new corresponding elements. The data_vectors are recreated as new_data_vectors and the data is copied for the unchanged elements, the values for the new elements resulting from refinement or coarsening are set to nan.

The user can also control where the nodes created by specifying the refinement_method. If refinement_method is ‘linear’, then the new node is created between the two nodes of the element. If it is ‘curved’, then the new node is created off the element along the normal from the midpoint of the element in a way to match the average curvature of the element.

Parameters

• curve (:obj:'Curve') –

• markers (NumPy array) – An array of integers, the same length as the curve size. It specifies if an element will be refined or coarsened. If markers[i] = 1, then element[i] will be refined. If markers[i] = -1, then element[i] will be coarsened. If markers[0] = 0, then element[i] will remain the same.

• data_vectors (list of NumPy arrays) – Each of the arrays in the list should be the same length as the size of the curve, for example, the arrays can be of size C or (n1,C) or (n1,n2,C), C being the curve size. The data vectors represent data associated with elements. They will remapped and reassigned to match the new indices of the elements.

• refinement_method (str) – The refinement method specifies where the new node will be created. Its value is one of ‘linear’ or ‘curved’. If refinement_method is ‘linear’, then the new node is created between the two nodes of the element. If refinement_method is ‘curved’, then the new node is created off the element along the normal from the midpoint of the element in a way to match the average curvature of the element.

Returns

• new_data_vectors (list of NumPy arrays) – The remapped data vectors created from the original data vectors, a list of NumPy arrays, storing the data associated with the new data. The values of the unchanged elements are copied to the new corresponding element indices. The data values for the new elements resulting from refinement and coarsening are set to nan.

• new_indices (NumPy array) – An array of integers giving the indices/locations of the new elements.

skshape.geometry.curve_examples module

class skshape.geometry.curve_examples.FlowerCurve(n, center=0.0, 0.0, radius=1.0, amplitude=0.25, frequency=4.0)

Bases: skshape.geometry.curve.Curve

exact_coords(s, param=None)

exact_curvature(s, param=None)

exact_normals(s, param=None)

exact_second_fund_form(s, param=None)

exact_tangents(s, param=None)

class skshape.geometry.curve_examples.GeneralizedCircle(n, center=0.0, 0.0, radius=1.0, p=2)

Bases: skshape.geometry.curve.Curve

exact_coords(s, param=None)

exact_curvature(s, param=None)

exact_normals(s, param=None)

exact_second_fund_form(s, param=None)

exact_tangents(s, param=None)

class skshape.geometry.curve_examples.GeneralizedEllipse(n, center=0.0, 0.0, axes=1.0, 1.0, p=2)

Bases: skshape.geometry.curve.Curve

exact_coords(s, param=None)

class skshape.geometry.curve_examples.Limacon(n, center=0.0, 0.0, radius=1.5)

Bases: skshape.geometry.curve.Curve

exact_coords(s, param=None)

exact_curvature(s, param=None)

exact_normals(s, param=None)

exact_second_fund_form(s, param=None)

exact_tangents(s, param=None)

skshape.geometry.curve_examples.curve_example(curve_id, n=8, center=[0.0, 0.0], radius=1.0, parameters={})

Creates a discretized example of the specified curve.

Creates the specified example curve discretized n nodes. The curve can be a square, rectangle, circle, ellipse, limacon, flower.

Parameters

• curve_id (str) – One of ‘square’, ‘rectangle’, ‘circle’, ‘ellipse’, ‘limacon’, ‘flower’

• n (int, optional) – The number of points used to discretize the curve example.

• center (array_like, optional) – The center of the curve. Default value is [0.0,0.0].

• radius (float, tuple, optional) – Radius or (height, width) of the curve. Default value is 1.0.

• parameters (dict, optional) – A dictionary of parameters specific to the curve type.

Returns

curve

Return type

object, Curve, Limacon, FlowerCurve, GeneralizedCircle, GeneralizedEllipse

skshape.geometry.domain module

class skshape.geometry.domain.Domain2d(curves=None, triangles=None, vertices=None)

Bases: skshape.geometry._mesh.Mesh

area()

coords(mask=None)

copy()

dim()

dim_of_world()

element_sizes(mask=None)

mark_grid(grid, origin=0.0, 0.0, size=1.0, 1.0, value=1)

mesh(curves, options='p')

refine_coarsen(markers, data_vectors=[], conforming=False)

reset_data()

show(tri=None, vtx=None, mask=None, format='k-', factor=1.0)

size()

triangles()

vertices()

volume()

skshape.geometry.grid module

class skshape.geometry.grid.Grid2d(resolution, origin=0.0, 0.0, size=1.0, 1.0)

Bases: skshape.geometry._mesh.Mesh

dim()

dim_of_world()

mark_inside_outside(curves)

Module contents

class skshape.geometry.Curve(coords, adaptivity_parameters={})

Bases: skshape.geometry._mesh.Mesh

Lagrangian curve discretized as a list of nodes, and geometric functions.

Curve class encapsulating the data and functionality for a Lagrangian curve discretized as a list of nodes on the (x,y) plane. The geometric functions include normal, curvature computation, interior area and other functions.

adapt(parameters=None)

area()

bounding_box()

contains(obj)

coords()

copy(copy_cache_data=False)

curvature(s=None, mask=None, coarsened=False)

Computes the curvature of the curve.

Computes the curvature at the node i by fitting a circle to nodes i-1, i, i+1 and computing its radius r. Then the curvature is given by 1/r. The curvature values between the nodes are given by linear interpolation.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the curvature is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the curvature values are sought.

• coarsened (bool, optional) – True if the curvature values are sought for coarsened elements, otherwise False.

Returns

curvature – A NumPy array storing the computed curvature values.

Return type

NumPy array

dim()

dim_of_world()

edges()

element_sizes(mask=None, coarsened=False, squared=False)

exterior_area(world_boundary=None)

exterior_volume(world_boundary=None)

interior_area(world_boundary=None)

interior_volume(world_boundary=None)

length()

move(update, adaptivity=None, world_boundary=None)

move_back()

normals(s=None, mask=None, coarsened=False, smoothness='pwconst')

Computes the unit normals of the curve.

Returns the normal vectors for the elements of a curve (the pwconst case) or for the nodes of the curve (the pwlinear case). In the piecewise constant case, the normals are given by the difference of the first and second nodes of the element, i.e.

In the piecewise linear case, the normals are computed as weighted averages of the element normals. The normal vectors are normalized to have unit length.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the normal is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the normals are sought.

• coarsened (bool, optional) – True if the normals are sought for coarsened elements, otherwise False.

• smoothness (str, optional) – An optional flag denoting the smoothness of the computed normals. Its value can be ‘pwconst’, corresponding to piecewise constant normals defined on the elements, (but not on the nodes) or its value can be ‘pwlinear’, corresponding to piecewise linear normals, defined by coefficients on the nodes and by interpolation of the coefficients on the edges.

Returns

normals – A NumPy array of size 2xN storing the x and y components of the normals.

Return type

NumPy array

orientation()

Returns the orientation of the curve.

Computes the signed area of the curve, and returns the orientation of the curve based on the area. If area > 0, then orientation is 1. If area < 0, then orientation is -1. If area = 0, then orientation is 0.

Returns

orientation_value

Return type

int, one of -1,0,1

refine_coarsen(mask, data_vecs, refinement_method='curved')

reset_data()

reverse_orientation()

safe_step_size(V, tol=0.3)

The maximum safe step size to avoid local geometric distortions.

If the spacing between the two nodes of an element changes too rapidly, this might create distortions in the geometric representation. This function computes the maximum safest step size to move the curve with the given velocity. The computation is based on the following inequality to be enforced

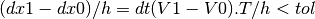
where dx1, dx0 denote the changes in the node locations, V1, V0 are their velocity, h is the size, T is the tangent vector of the element.

Parameters

• V (NumPy array) – The velocity vector, a NumPy array of size (2,n), where n is the number of nodes of the curve.

• tol (float) – Allowed ratio of relative tangential displacement with respect to the element size. The default value is 0.3.

Returns

dt – The maximum safe step size allowed within the specified tolerance.

Return type

float

second_fund_form(s=None, mask=None, coarsened=False)

Estimates the second fundamental form on nodes of the curve.

Estimates the second fundamental form on each element using the following formula:

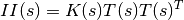
where K(s) is the scalar curvature, interpolated linearly from nodal curvature values, T(s) is piecewise linear reconstruction of the unit tangent vector, T(s)^T is its transpose. The second fundamental curve can be computed for nodes of the curve or interior points of the elements denoted by s, on all elements or selected elements specified by mask. They can be computed for coarsened elements too.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the second fundamental form is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the values of the second fundamental form are sought.

• coarsened (bool, optional) – True if the values of the second fundamental form are sought for coarsened elements, otherwise False.

Returns

II – An array of size 2x2xN storing the components of the second fundamental form.

Return type

NumPy array

set_adaptivity(adaptivity=True)

Turns on/off mesh adaptivity.

This function is used to switch mesh adaptivity on or off.

Parameters

adaptivity (bool) – A boolean argument to set mesh adaptivity to True or False.

set_data_adaptivity_criteria(refinement_functions=None, coarsening_functions=None, append=False)

Sets data adaptivity criteria given for refinement and coarsening.

Curves can be adapted spatially (refined or coarsened) with respect to given criteria. This function is used to set or add a refinement or coarsening pair (of error and marking functions) to the criteria list. The curve’s criteria list includes the geometric criterion by default (if created with default arguments).

The geometric criterion estimates the geometric error by examining the curvatures and element sizes of the curves. Then the marking function marks the elements with errors above a certain threshold for refinement. See the following function for more information:

geometry.curve_adaptivity.compute_geometric_error(...)

If new refinement or coarsening error functions are added or appended, then mesh_adaptivity is turned on. To turn it off, you need to call the function: set_adaptivity(False).

Parameters

• refinement_functions –

  A pair of pairs storing the error estimation function and the corresponding marking function to drive refinement of elements. It has the following format:

  ( error_estimation_pair, marking_pair )

  where

  error_estimation_pair = (error_func, error_params)

  and

  marking_pair = (marking_func, marking_params).

  The error estimation function should have the curve as an argument and three other optional arguments: mask, a boolean NumPy array or an integer NumPy array of element indices, vec, a float NumPy array to store the error values, parameters, a dictionary of parameters needed for error estimation. The default for these three arguments can be None. An example is

  compute_geometric_error(curve, mask=None, vec=None,

  parameters=None)

  Marking functions are defined in the module geometry.marking.

• coarsening_functions – A pair of pairs storing the error estimation function and the corresponding marking function to drive coarsening of elements. Its format is the same as that of refinement functions.

• append (bool, optiomal) – A boolean optional flag with default value equal to False. If it is True, the given criteria are appended to the existing list and all the criteria in the list are used together. If it is False, only the first geometric criteria (if they are available) are kept in the refinement and coarsening criteria list, the others in the lists are removed and the new ones are inserted.

set_geometry(coords, element_sizes=None, normals=None, curvature=None)

set_orientation(new_orientation)

show(format='b', factor=1.0)

size()

surface_area()

tangents(s=None, mask=None, coarsened=False, smoothness='pwconst')

Computes the unit tangents of the curve.

Returns the tangent vectors for the elements of a curve (the pwconst case) or for the nodes of the curve (the pwlinear case). In the piecewise constant case, the tangents are given by the difference of the first and second nodes of the element, i.e.

In the piecewise linear case, the tangents are computed as weighted averages of the element tangents. The tangent vectors are normalized to have unit length.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the tangent is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the tangents are sought.

• coarsened (bool, optional) – True if the tangents are sought for coarsened elements, otherwise False.

• smoothness (str, optional) – An optional flag denoting the smoothness of the computed tangents. Its value can be ‘pwconst’, corresponding to piecewise constant tangents defined on the elements, (but not on the nodes) or its value can be ‘pwlinear’, corresponding to piecewise linear tangents, defined by coefficients on the nodes and by interpolation of the coefficients on the edges.

Returns

tangents – A NumPy array of size 2xN storing the x and y components of the tangents.

Return type

NumPy array

volume()

class skshape.geometry.CurveHierarchy(curve_list, world_boundary=None, curve_hierarchy=None, adaptivity_parameters={})

Bases: skshape.geometry._mesh.Mesh

Hierarchy of nonintersecting simple curves on the (x,y) plane.

This class stores the hierarchy and spatial positioning of a set of nonintersecting simple curves on (x,y) planes. It stores the list of the Curve objects as well. In this way, it can perform the geometric computations, e.g. curvature, normals for all the curves.

adapt(parameters=None)

add_remove_curves(remove_curve_ids, new_curve_list, recompute_parent_list=[], enforce_consistency=True)

area()

coords()

copy(copy_cache_data=False)

curvature(s=None, mask=None, coarsened=False)

Computes the curvature of the curves in the CurveHierarchy.

Computes the curvature at the node i by fitting a circle to nodes i-1, i, i+1 and computing its radius r. Then the curvature is given by 1/r. The curvature values between the nodes are given by linear interpolation.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the curvature is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the curvature values are sought.

• coarsened (bool, optional) – True if the curvature values are sought for coarsened elements, otherwise False.

Returns

curvature – A NumPy array storing the computed curvature values.

Return type

NumPy array

curve_hierarchy()

curve_list()

dim()

dim_of_world()

edges()

element_sizes(mask=None, coarsened=False, squared=False)

exterior_area(world_boundary=None)

exterior_domain(world_boundary=None)

exterior_volume(world_boundary=None)

get_curve_object(curve_id)

has_submeshes()

hole_points()

interior_area(world_boundary=None)

interior_domain(world_boundary=None)

interior_volume(world_boundary=None)

length()

local_to_global(s, mask=None, coarsened=False)

move(update, adaptivity=None, world_boundary=None)

move_back()

normals(s=None, mask=None, coarsened=False, smoothness='pwconst')

Computes the unit normals of the curve family.

Returns the normal vectors for the elements of the curves (the pwconst case) or for the nodes of the curves (the pwlinear case). In the piecewise constant case, the normals are given by the difference of the first and second nodes of the element, i.e.

In the piecewise linear case, the normals are computed as weighted averages of the element normals. The normal vectors are normalized to have unit length.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the normal is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the normals are sought.

• coarsened (bool, optional) – True if the normals are sought for coarsened elements, otherwise False.

• smoothness (str, optional) – An optional flag denoting the smoothness of the computed normals. Its value can be ‘pwconst’, corresponding to piecewise constant normals defined on the elements, (but not on the nodes) or its value can be ‘pwlinear’, corresponding to piecewise linear normals, defined by coefficients on the nodes and by interpolation of the coefficients on the edges.

Returns

normals – A NumPy array of size 2xN storing the x and y components of the normals.

Return type

NumPy array

orientation()

refine_coarsen(mask, data_vecs, refinement_method='curved')

region_areas(world_boundary=None)

region_volumes(world_boundary=None)

regions()

reset_data()

reverse_orientation()

safe_step_size(V, tol=0.3)

The maximum safe step size to avoid local geometric distortions.

If the spacing between the two nodes of an element changes too rapidly, this might create distortions in the geometric representation. This function computes the maximum safest step size to move the curve with the given velocity. The computation is based on the following inequality to be enforced

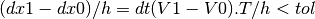
where dx1, dx0 denote the changes in the node locations, V1, V0 are their velocity, h is the size, T is the tangent vector of the element.

Parameters

• V (NumPy array) – The velocity vector, a NumPy array of size (2,n), where n is the number of nodes of the curve.

• tol (float) – Allowed ratio of relative tangential displacement with respect to the element size. The default value is 0.3.

Returns

dt – The maximum safe step size allowed within the specified tolerance.

Return type

float

second_fund_form(s=None, mask=None, coarsened=False)

Estimates the second fundamental form on nodes of the curves.

Estimates the second fundamental form on each element using the following formula:

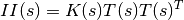
where is the scalar curvature, interpolated linearly from nodal curvature values, 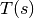is piecewise linear reconstruction of the unit tangent vector, 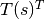is its transpose. The second fundamental curve can be computed for nodes of the curve or interior points of the elements denoted by s, on all elements or selected elements specified by mask. They can be computed for coarsened elements too.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the second fundamental form is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the values of the second fundamental form are sought.

• coarsened (bool, optional) – True if the values of the second fundamental form are sought for coarsened elements, otherwise False.

Returns

II – An array of size 2x2xN storing the components of the second fundamental form.

Return type

NumPy array

set_adaptivity(adaptivity=True)

Turns on/off mesh adaptivity.

This function is used to switch mesh adaptivity on or off.

Parameters

adaptivity (bool) – A boolean arguments to set mesh adaptivity to True or False.

set_boundary(world_boundary)

set_data_adaptivity_criteria(refinement_functions=None, coarsening_functions=None, append=False)

Sets data adaptivity criteria given for refinement and coarsening.

Curves can be adapted spatially (refined or coarsened) with respect to given criteria. This function is used to set or add a refinement or coarsening pair (of error and marking functions) to the criteria list. The curve’s criteria list includes the geometric criterion by default (if created with default arguments).

The geometric criterion estimates the geometric error by examining the curvatures and element sizes of the curves. Then the marking function marks the elements with errors above a certain threshold for refinement. See the following function for more information:

geometry.curve_adaptivity.compute_geometric_error(...)

If new refinement or coarsening error functions are added or appended, then mesh_adaptivity is turned on. To turn it off, you need to call the function: set_adaptivity(False).

Parameters

• refinement_functions –

  A pair of pairs storing the error estimation function and the corresponding marking function to drive refinement of elements. It has the following format:

  ( error_estimation_pair, marking_pair )

  where

  error_estimation_pair = (error_func, error_params)

  and

  marking_pair = (marking_func, marking_params).

  The error estimation function should have the curve as an argument and three other optional arguments: mask, a boolean NumPy array or an integer NumPy array of element indices, vec, a float NumPy array to store the error values, parameters, a dictionary of parameters needed for error estimation. The default for these three arguments can be None. An example is

  compute_geometric_error(curve, mask=None, vec=None,

  parameters=None)

  Marking functions are defined in the module geometry.marking.

• coarsening_functions – A pair of pairs storing the error estimation function and the corresponding marking function to drive coarsening of elements. Its format is the same as that of refinement functions.

• append (bool, optional) – A boolean optional flag with default value False. If it is True, the given criteria are appended to the existing list and all the criteria in the list are used together. If it is False, only the first geometric criteria (if they are available) are kept in the refinement and coarsening criteria list, the others in the lists are removed and the new ones are inserted.

set_orientation(new_orientation)

set_topology_changes(value=True)

show(format='b', factor=1.0)

size()

submeshes()

surface_area()

tangents(s=None, mask=None, coarsened=False, smoothness='pwconst')

Computes the unit tangents of the curve family.

Returns the tangent vectors for the elements of the curves (the pwconst case) or for the nodes of the curves (the pwlinear case). In the piecewise constant case, the tangents are given by the difference of the first and second nodes of the element, i.e.

In the piecewise linear case, the tangents are computed as weighted averages of the element tangents. The tangent vectors are normalized to have unit length.

Parameters

• s (float, optional) – An optional local coordinate, a value between 0 and 1. This needs to be given if the value of the tangent is sought at a local position, say s=0.2, on all elements. Its default value is None.

• mask (NumPy array, optional) – A NumPy array of integer indices, indicating the elements for which the tangents are sought.

• coarsened (bool, optional) – True if the tangents are sought for coarsened elements, otherwise False.

• smoothness (str, optional) – An optional flag denoting the smoothness of the computed tangents. Its value can be ‘pwconst’, corresponding to piecewise constant tangents defined on the elements, (but not on the nodes) or its value can be ‘pwlinear’, corresponding to piecewise linear tangents, defined by coefficients on the nodes and by interpolation of the coefficients on the edges.

Returns

tangents – A NumPy array of size 2xN storing the x and y components of the tangents.

Return type

NumPy array

topmost_curve_ids()

volume()

class skshape.geometry.Domain2d(curves=None, triangles=None, vertices=None)

Bases: skshape.geometry._mesh.Mesh

area()

coords(mask=None)

copy()

dim()

dim_of_world()

element_sizes(mask=None)

mark_grid(grid, origin=0.0, 0.0, size=1.0, 1.0, value=1)

mesh(curves, options='p')

refine_coarsen(markers, data_vectors=[], conforming=False)

reset_data()

show(tri=None, vtx=None, mask=None, format='k-', factor=1.0)

size()

triangles()

vertices()

volume()

class skshape.geometry.Grid2d(resolution, origin=0.0, 0.0, size=1.0, 1.0)

Bases: skshape.geometry._mesh.Mesh

dim()

dim_of_world()

mark_inside_outside(curves)

skshape.geometry.curve_example(curve_id, n=8, center=[0.0, 0.0], radius=1.0, parameters={})

Creates a discretized example of the specified curve.

Creates the specified example curve discretized n nodes. The curve can be a square, rectangle, circle, ellipse, limacon, flower.

Parameters

• curve_id (str) – One of ‘square’, ‘rectangle’, ‘circle’, ‘ellipse’, ‘limacon’, ‘flower’

• n (int, optional) – The number of points used to discretize the curve example.

• center (array_like, optional) – The center of the curve. Default value is [0.0,0.0].

• radius (float, tuple, optional) – Radius or (height, width) of the curve. Default value is 1.0.

• parameters (dict, optional) – A dictionary of parameters specific to the curve type.

Returns

curve

Return type

object, Curve, Limacon, FlowerCurve, GeneralizedCircle, GeneralizedEllipse

skshape.geometry.triangulation_from_labels(image, smooth_boundaries=True, coarsen_boundaries=True)

Creates a triangulation for the regions of the labeled image.

This function identifies the regions in a given labeled image, extracts the boundary curves between regions, and creates a triangulation the conforms to the regions.

Parameters

• image (NumPy array) – An image of pixels labels

• smooth_boundaries (bool, optional) – Boolean flag that determines whether or not the region boundary curves will be smoothed. Default value is True.

• coarsen_boundaries (bool, optional) – Boolean flag that determines whether or not the region boundary curves will be coarsened. Default value is True.

Returns

• boundary_curves (list of NumPy arrays) – List of region boundary curves stores in two-row arrays.

• tri_nodes (NumPy array) – (3,n)-sized array of floats, storing the coordinates of all the nodes in the triangulation.

• triangles (NumPy array) – (3,nT)-sized array of integers, storing the nodes of the triangles.