Here are some examples of projects that I have been working on:

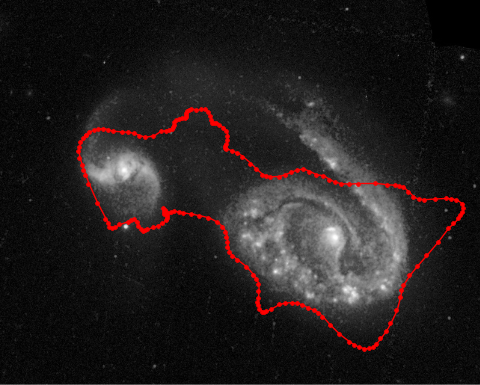
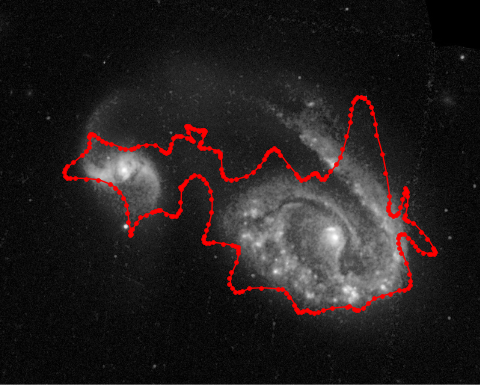
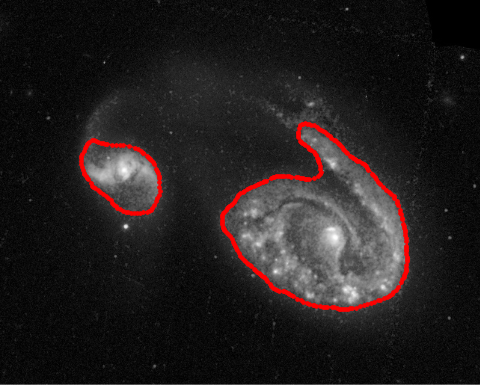
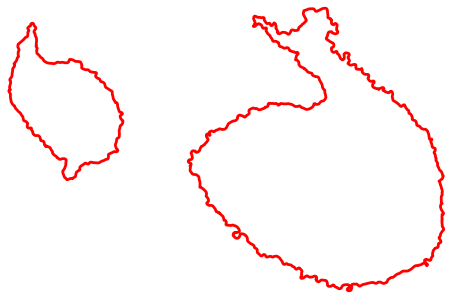
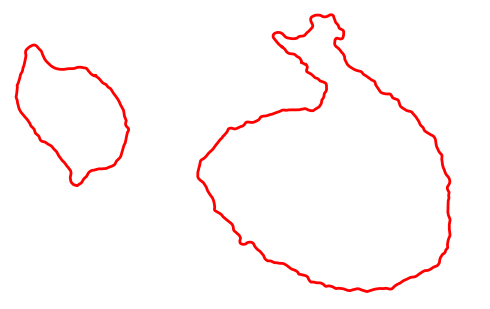
Image segmentation with deformable curves

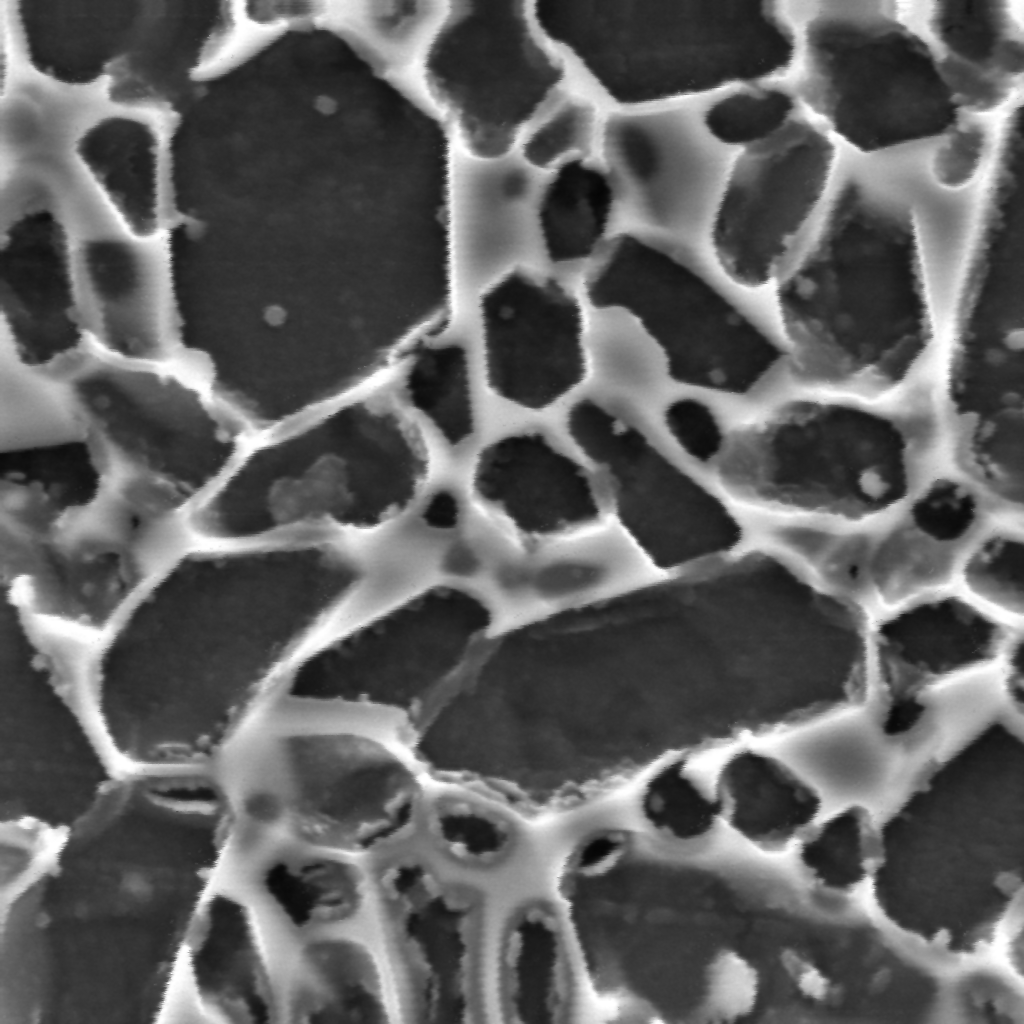
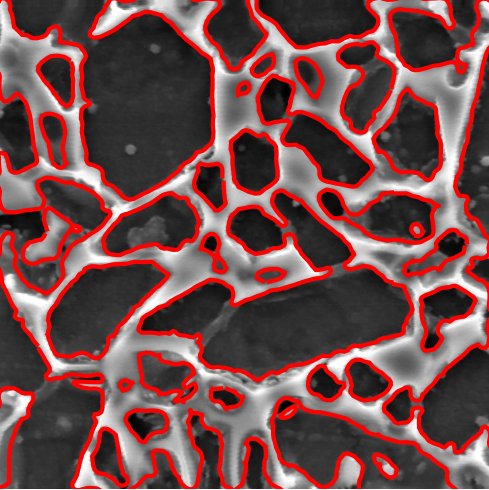
Segmentation and meshing complex domains in material microstructures

Geometric regularization of object boundaries in segmentation

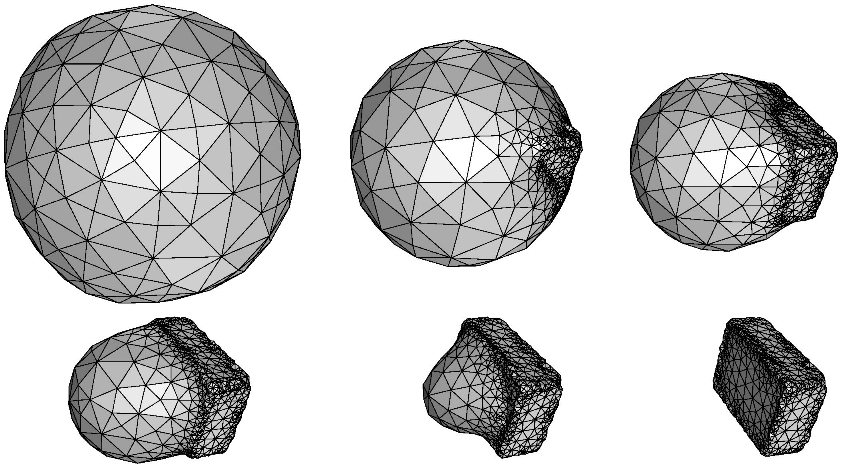
Adaptive triangulated surfaces for 3d object detection

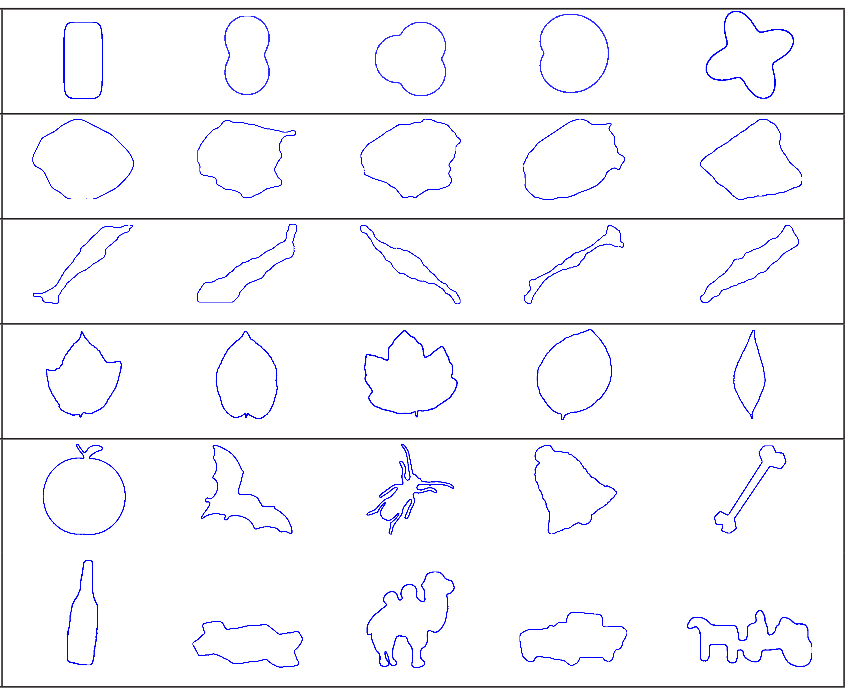
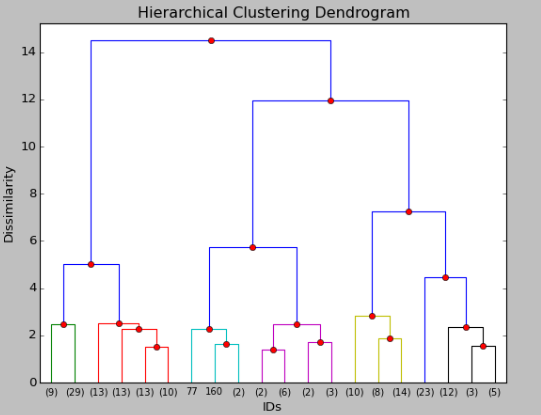
Elastic shape distances for large-scale statistical shape analysis

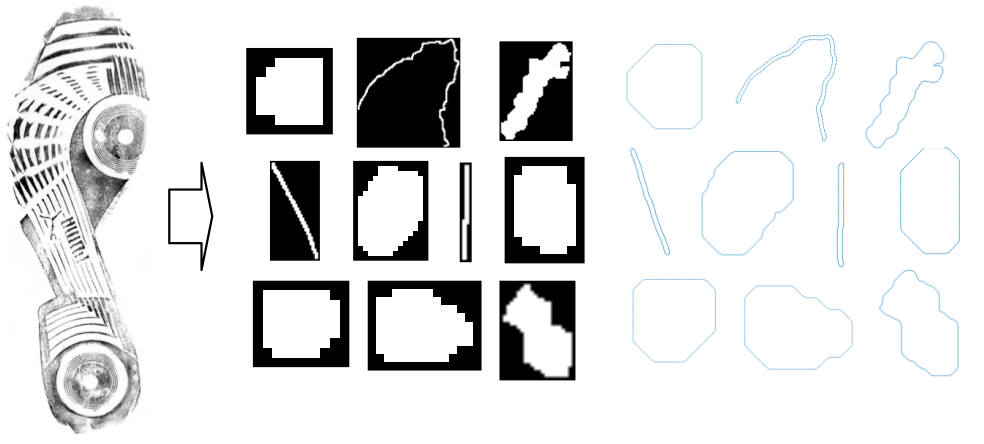
Detection and analysis geometric features and patterns in shoeprint forensics